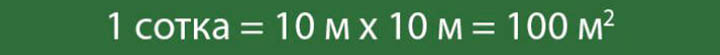Погрешность определения площади земельного участка формула

Расположение поворотных точек границ земельного участка

При покупке нового участка человек часто сталкивается с проблемой определения точных координат своей земли. Так, поворотные точки границ земельного участка являются главным фактором для определения местоположения землевладения. Правильно расставленные поворотные точки позволяют в кратчайшие сроки провести межевание и приступить к строительству или иным работам по благоустройству территории.

Рекомендуем прочесть: Когда Блокируется Транспортная Карта

Поворотные точки границ надела: это что такое и зачем нужны

Итак, каждый земельный удел должен пройти регистрацию в государственных органах контроля, а также получить кадастровый номер с занесением в специальную книгу. Кстати, координаты поворотных точек границ земельного участка позволяют скорым образом провести разграничение и указать территорию, на которой в дальнейшем будет хозяйствовать застройщик.

Когда соседи не готовы к мирному диалогу относительно спорных границ, единственный вариант – обращение в суд. Такой подход потребует времени, дополнительных затрат, но решение суда окончательно поставит точку в споре. Нужно быть готовым к тому, что вам все равно придется проводить землеустроительную экспертизу, так как в делах по земельным спорам она назначается практически всегда.

Точность прибора. Для определения координат используют геодезическое оборудование, которое должно регулярно проходить проверки. К сожалению, гарантировать, что оборудование дает минимальную погрешность, могут только крупные специализированные компании. Небольшие компании или частные специалисты не имеют своего оборудования и проводят замеры арендованными приборами. Погрешность в таком случае может сильно выходить за допустимые пределы.
Метод измерений. В геодезии используют разные методы, и все они дают разную погрешность.
Квалификация специалиста. Тот факт, что частный специалист имеет лицензию, совершенно не подтверждает его высокую квалификацию. Рекомендуем вам перед заключением договора проверять на сайте Росреестра не только информацию о лицензиях и допусках, но и количество отказов

Обращаясь в , вы можете быть уверены в квалификации и, что тоже немаловажно, опыте кадастрового инженера, который будет заниматься вашим вопросом.

Как определить границы земельного участка?

Местоположение фактической границы может колебаться в пределах установленной нормы, и это не является нарушением закона. Но и здесь все не так просто, как может показаться. Дело в том, что до 2013 года существовали другие нормы погрешности. Так, например, для садоводческих участков, земель ЛПХ норма устанавливалась в 0,3 метра.

1. Для ЗУ расположенных в населённых пунктах – не более 10 см.
2. Для земель сельхоз назначения: предназначенных для ведения ЛПХ, ИЖС, дач, садов, огородов, подсобных строений (гаражей) – не более 20 см.
3. Для земель сельхоз назначения, за исключением перечисленных выше – до 2 метров с половиной.
4. Для ЗУ, где расположены промышленные предприятия различного типа и назначения, проходят транспортные линии, энергетические объекты. А также для ЗУ оборонной промышленности, специального назначения и аналогичных назначений – до полуметра.
5. Земли: лесного, водного фондов и запаса – до 5 метров.

Допустимые погрешности межевания определяются категорией земель и её предназначением. Это играет существенную практическую роль. Огромные земельные массивы, относящиеся к фондам лесов или водных пространств, естественно, не потребуют такой достоверности как, например, участки под ИЖС или дачные участки.

Точность и погрешность

Каждая точка определяется в системе пересечения координат X и Y, в результате чего определяется её максимально точное местоположение в пространстве. В указанной форме даются сведения о местонахождении координат каждой поворотной точки, в отношении всех имеющихся в межевом деле ЗУ поворотных точек участка.

В левом верхнем углу ПКК расположено окно поиска. В нем следует выбрать раздел «Участки» и вписать в пустующее поле кадастровый номер. После нажатия кнопки «Найти» границы нужного участка будут выделены желтым цветом. Площадь и адрес объекта можно увидеть в окне слева.

Cпособы определения площадей в геодезии

Определение площадей земельных участков является одним из важнейших видов геодезических работ для целей земельного кадастра.

В зависимости от хозяйственной значимости земельных участков, наличия планово-топографического материала, топографических условий местности и требуемой точности применяют различные способы определения площадей.

1. Аналитический, когда площадь вычисляется по результатам измерений линий на местности, по результатам измерений линий и углов на местности или по их функциям (координатам вершин фигур).

2. Графический, когда площадь вычисляется по результатам измерений линий или координат на плане (карте). Графические способы. Участок на плане разбивают на простые геометрические фигуры (обычно – треугольники), элементы которых измеряют с помощью измерителя и поперечного масштаба, а площади вычисляют по известным формулам и суммируют.

3. Механический, когда площадь определяется по плану с помощью специальных приборов (планиметров) или приспособлений (палеток). Иногда эти способы применяют комбинированно, например, часть линейных величин для вычисления площади определяют по плану, а часть берут из результатов измерений на местности.

Площади можно также определить на ЭВМ по цифровой модели местности по специальной программе.

При аналитическом способе определения площадей применяются формулы геометрии, тригонометрии и аналитической геометрии. При определении площадей небольших участков (для учета площадей, занятых строениями, усадьбами, площадей вспашки, посева) участки разбиваются на простейшие геометрические фигуры, преимущественно треугольники, прямоугольники, реже трапеции. В этом случае площади участков определяются как суммы площадей отдельных фигур, вычисляемых по линейным элементам — высотам и основаниям.

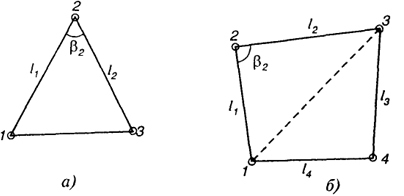
а, б

Если по границам участка выполнены геодезические измерения, то площадь всего участка или его части можно вычислить по формулам, приведенным применительно к следующим фигурам участков (рис. 23.1).

Треугольник (рис. 23.1, а). Площадь треугольника определяется по сторонам l₁ и l₂, углу β₂, заключенному между ними, по формуле

Четырехугольник (рис. 23.1, б). В зависимости от элементов, известных в четырехугольнике, могут быть использованы различные формулы для расчета, в связи с чем приведем пример, характеризующий это многообразие. Пусть в четырехугольнике измерены все стороны и один угол при вершине 2. В таком случае площадь треугольника 1 — 2 — 3 может быть вычислена по формуле (23.1). При этом полезно вычислить длину l_1-3, используя теорему косинусов

Площадь треугольника 1 — 3 — 4 может быть вычислена по формуле

где S — полупериметр, равный

Общая площадь четырехугольника будет равна:

Источник

Обозначение площади

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Если параметры фигуры переданы в разных единицах длины, мы не сможем решить ни одну задачу. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения

• квадратный миллиметр (мм 2 );
• квадратный сантиметр (см 2 );
• квадратный дециметр (дм 2 );
• квадратный метр (м 2 );
• квадратный километр (км 2 );
• гектар (га).

Круг — это когда множество точек на плоскости удалены от центра на равном радиусу расстоянии. Радиусом принято называть прямую линию, соединяющую центр с любой точкой окружности.

1. S = π * r 2 , где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

2. S = d 2 : 4 * π, где d — это диаметр.

3. S = L 2 ​ : 4 * π, где L — это длина окружности.

СПОСОБЫ ОПРЕДЕЛЕНИЯ ПЛОЩАДИ

Процесс определения площади земельных участков или любых других объектов недвижимости включает следующие этапы:

1. Выполнение измерений при помощи различных технических средств;

2. Вычислительная обработка результатов измерений;

3. Составление экспликации по площадям угодий (сводные данные).

В зависимости от формы земельных участков и используемых технических средств применяют следующие способы определения площадей:

1. Аналитический – основан на вычислении площади по результатам измерений линий и углов на местности с применением формул геометрии и тригонометрии, а также по координатам вершин точек поворота границы земельного участка;

2. Графоаналитический – основан на вычислении площади по результатам измерений на плане. Участок разбивается на простейшие геометрические фигуры или измерения производятся при помощи палеток;

3. Механический – основан на измерении площадей на плане или карте при помощи планиметров.

Наиболее точен аналитический способ, так как здесь сказываются только ошибки измерений на местности. Он требует большого объёма вычислений. Хотя при наличии карт на цифровых носителях и современной вычислительной техники это не имеет особого значения.

Наиболее распространён благодаря скорости и простоте определения площадей на бумажных носителях механический способ. Хотя он менее точен.

Графический способ есть смысл применять, когда граница прямолинейна и имеет малое число поворотов, или площадь участка на плане менее 3 см. Для определения площади земельного участка, границы которого имеют прямолинейные очертания и большое число точек поворота, деление на треугольники нежелательно. Более предпочтительным вариантом является вычисление площади по координатам точек поворота границы землепользования. Координаты точек поворота графически снимаются при помощи циркуля-измерителя и определяются по линейке поперечного масштаба.

studopedia.ru

Требования к точности

После обозначения поворотных точек проводят границы участка в виде прямых линий. Любые неровности, наличие растительности усложняют процесс прокладки ровных линий. Нельзя исключать человеческий фактор и неисправность работы измерительных приборов.

Новая рассчитанная площадь и уточненные на ней границы не могут превышать показатели, указанные в кадастровом документе ЗУ, больше, чем на установленные законом нормы.

На площадях большого размера, например сельскохозяйственных угодий, нанести контуры угодий достаточно сложно. По этой причине, существует установленный допустимый показатель погрешности и требования к точности приборов.

После исследования, инженер обязан провести согласование границ с владельцами соседних участков на специальном собрании. Всех участников в обязательном порядке уведомляют в письменном виде. Все извещения вручают под личную подпись.

В случае отсутствия соседей, в местных средствах массовой информации публикуют уведомление. Данную процедуру может взять на себя межующая компания или владелец участка.

Всех участников собрания для получения согласования необходимо предварительно уведомить о том, что будет проводиться процедура определения границ.

Минимальный срок — за 30 календарных дней до момента осуществления измерений.

Результатом работ является составленное землеустроительное дело, которое передают в землеустроительную организацию для согласования межевого плана.

Геометрический способ

Существует три способа определения площади участков: геометрический, аналитический и механический. На местности применяют два первых способа, на картах и планах – все три способа.

Геометрический способ – это вычисление площади геометрических фигур по длинам сторон и углам между ними, значения которых можно получить только из измерений.

Сначала рассмотрим простейшую фигуру – треугольник.

Формулы для вычисления площади треугольника известны:

P = 0.5 * a * h;                       (6.1)

P = 0.5 * a * b * Sin(C)                           (6.2)

(6.3)

в этих формулах:
a, b, c – длины сторон треугольника,
A, B, C – углы при вершинах против соответствующих сторон,
h – высота, проведенная из вершины A на сторону a,
p – полупериметр, p=0.5*(a + b + c).

Для решения любого n-угольника нужно знать (2*n – 3) его элементов, причем количество известных углов не должно быть больше (n-1), так как один угол всегда может быть вычислен, если остальные углы известны, на основании формулы:

β = 180 * ( n – 2 )                          (6.4)

При расчете ошибки определения площади следует учитывать ошибки всех (2n-3) измеряемых элементов.

В треугольнике нужно знать (измерить) три элемента. Формула (6.1) содержит всего два элемента; это значит, что прямой угол между основанием и высотой нужно отдельно обеспечить с необходимой точностью, что равнозначно одному измерению.

Примем относительную ошибку площади mp/P = 1/1000, тогда для применения формулы (6.1) на основании принципа равных влияний необходимо выполнить условия:

и

где ma,mb,β – ср.кв. ошибки сторон a, b и прямого угла между основанием и высотой.

Для формулы (6.2) на основании принципа равных влияний можно написать:

(6.5)

Считая попрежнему mp/P=1/1000, получим:

и  mβ= 3.4′ при < C = 60,
mβ= 2.0′ при < C = 45,
mβ= 1.0′ при < C = 26.

Если в треугольнике измерять три стороны с относительной ошибкой mS/S и для вычисления площади применять формулу (6.3), то для равностороннего треугольника получим:

(6.6)

что при mp/P=1/1000 дает ms/S=1/1500.

Таким образом, вариант с измерением трех сторон треугольника оказывается самым эффективным, так как в нем не требуется измерять углы.

Четырехугольник, как геометрическая фигура, может быть параллелограммом, ромбом, трапецией, прямоугольником, квадратом; но как участок местности его следует считать фигурой произвольной формы, так как обеспечение геометрических свойств той или иной фигуры на местности требует дополнительных измерений.

В четырехугольнике (n=4) нужно измерить пять элементов: три угла и две стороны или два угла и три стороны или один угол и четыре стороны или четыре стороны и одну диагональ. Последний вариант является наиболее предпочтительным, так как, во-первых, в нем не нужно измерять углы, и, во-вторых, согласно формуле:

(6.7)

относительная ошибка площади примерно равна относительной ошибке измерения сторон. Во всех остальных вариантах при оценке точности площади нужно учитывать как ошибки измерения сторон, так и ошибки измерения углов.

Применение геометрического способа на местности требует разбиения участка на простые геометрические фигуры, что возможно лишь при наличии видимости внутри участка (рис.6.1.)

При определении площади участков на топографических планах и картах стороны и высоты треугольников, стороны и диагонали четырехугольников нужно измерять с помощью поперечного масштаба.

Для определения площади на карте или плане геометрическим способом часто используют палетку – лист прозрачной бумаги, на котором нанесена сетка квадратов или параллельных линий. Палетку с квадратами накладывают на участок и подсчитывают, сколько квадратов содержится в данном участке; неполные квадраты считают отдельно, переводя затем их сумму в полные квадраты. Площадь участка вычисляют по формуле:

P=n*(a*M)2,                        (6.8)

где a – длина стороны квадрата,
M – знаменатель масштаба карты,
n – количество квадратов на участке.

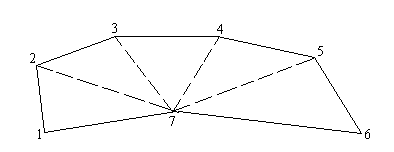
Рис.6.1

Рекомендовать Google:

Формулы площади выпуклого четырехугольника

Формула площади четырехугольника по длине диагоналей и углу между ними Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:

где S — площадь четырехугольника, d ₁, d ₂ — длины диагоналей четырехугольника, α — угол между диагоналями четырехугольника.

Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности) Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности

Формула площади четырехугольника по длине сторон и значению противоположных углов

a , b , c , d — длины сторон четырехугольника,

p = a + b + c + d 2 — полупериметр четырехугольника,

θ = α + β 2 — полусумма двух противоположных углов четырехугольника.

Формула площади четырехугольника, вокруг которого можно описать окружность

Какая допускается погрешность при межевании земельных участков

Фактические установление точных границ – это процедура межевания, проведенная по современным требованиям с применением современного геодезического оборудования. Уточнение позволяет достичь нескольких целей: Показатели Описание Сформировать точную границу участка на основании имеющихся координат Выявить границы всех смежных участков — Определить, нет ли наложения границ смежных ЗУ или слишком больших промежутков между ними Все эти вопросы относятся к разряду наиболее актуальных для владельцев земли. Кем проводится Уточнение границ земельного участка проводится специалистами геодезической компании, с которой заключен договор. Заинтересованный владелец ЗУ может обратиться к специалистам государственной или частной организации, которые имеют право проводить межевые работы.

Похожие:

	«Инженерная геодезия»…		П. С. Алексеев многопоточное программирование учебное пособие Санкт-Петербург 2010Санкт-петербургский государственный университет информационных технологий, механики и оптики
	Рабочая программа учебной дисциплины прикладная геодезия направление…«Землеустройство и кадастры», в соответствии с учебным планом, утвержденным ученым советом университета в 2016 году для очной формы…		Рабочая программа дисциплины «геодезия» основной образовательной…Рабочая программа обсуждена и одобрена на заседании кафедры «Кадастр и геодезия»
	Г. Санкт-Петербург 09. 09. 2014 гПредмет закупки: поставка бытовой техники: холодильников и микроволновых печей (далее Товар) в здания ниу вшэ – Санкт-Петербург,…		Литература по дисциплине «Цифровая обработка сигналов»Цифровая обработка сигналов : учебное пособие для вузов / А. Б. Сергиенко. 3-е изд. Санкт-Петербург : бхв петербург, 2011….
	Гуманитарныйинститу тОсновы генетики в коррекционной педагогике : учебное пособие для вузов / Л. А. Попова, Т. П. Степанова; под ред. В. П. Соломина….		Учебное пособие по устному и письменному переводу для переводчиков…Печатается по постановлению Редакционно-издательского совета Института иностранных языков (Санкт-Петербург)
	Учебное пособие для студентов высших учебных заведений по направлениям:…А. И. Подколзин, О. Ю. Лобанкова, Ю. И. Гречишкина, В. И., Радченко, А. А. Беловолова, Н. В. Громова, М. С. Сигида, С. А. Коростылев,…		Учебное пособие по дисциплине «Безопасность и природоохранные технологии…Учебно-методическое пособие предназначено для студентов высших учебных заведений, обучающихся по направлению 656600 «Защита окружающей…
	Владимирский Государственный Университет Научная библиотека Бюллетень…Принципы моделирования социальной самоорганизации: учебное пособие/ И. Д. Колесин. Санкт-Петербург: Лань, 2013. 281 c ил (Учебники…		Учебное пособие санкт-петербург 2016 ббк 65. 23 О 36 О36 Управление…Управление затратами труда на предприятии. Для бакалавров по направлению «Управление государственными и частными предприятиями» всех…
	Учебный план 3745 (еису) ифксиМП. 371. 62. 2015 Код ооп направление/……		Учебно-методическое пособие Санкт-Петербург 2014 Авторы: Морозов…Учебно-методическое пособие предназначено для повышения квалификации преподавательского состава умц по го чс и пб санкт-Петербурга…
	Учебное пособие модуль раздела 1 Геометрическое черчение раздела…Разработала Коновалова Л. М., преподаватель кафедры эдод (Экономических и деревообрабатывающих дисциплин)		Рабочая программа дисциплины б б. 5 Геодезия направление подготовки…Калюжин Виктор Анатольевич, заведующий кафедрой геоматики и инфраструктуры недвижимости, канд техн наук, доцент

Руководство, инструкция по применению

Инструкция, руководство по применению

Определение азимутов и дирекционных углов

Азимуты и дирекционные углы. Положение какого-либо объекта на местности чаще всего определяют и указывают в полярных координатах, то есть углом между начальным (заданным) направлением и направлением на объект и расстоянием до объекта. В качестве начального выбирают направление географического (геодезического, астрономического) меридиана, магнитного меридиана или вертикальной линии координатной сетки карты. За начальное может быть принято и направление на какой-нибудь удаленный ориентир. В зависимости от того, какое направление принято за начальное, различают географический (геодезический, астрономический) азимут А, магнитный азимут Ам, дирекционный угол a (альфа) и угол положения 0.

Географический (геодезический, астрономический) — это двугранный угол между плоскостью  меридиана данной точки и вертикальной плоскостью, проходящей в данном направлении, отсчитываемый от направления на север по ходу часовой стрелки (геодезический азимут представляет собой двугранный угол между плоскостью геодезического меридиана данной точки и плоскостью, проходящей через нормаль к ней и содержащей данное направление. Двугранный угол между плоскостью астрономического  меридиана данной точки и вертикальной плоскостью, проходящей в данном направлении,  называется астрономическим азимутом).

Магнитный азимут А 4м  — горизонтальный угол, отсчитываемый от северного направления магнитного меридиана по ходу часовой стрелки.

Дирекционный угол а — это угол между проходящим через данную точку направлением и линией, параллельной оси абсцисс, отсчитываемый от северного направления оси абсцисс по ходу часовой стрелки.

Все вышеперечисленные углы могут иметь значения от 0 до 360 .

Угол положения 0 измеряют в обе стороны от направления, принятого за начальное. Прежде чем назвать угол положения объекта (цели),  указывают, в какую сторону (вправо, влево) от начального направления он измерен.

Измерение длины маршрута

Длину маршрута измеряют по карте обычно курвиметром. Стандартный курвиметр имеет две шкалы для измерения расстояний по карте: с одной стороны метрическую (от 0 до 100 см), с другой стороны дюймовую (от 0 до 39,4 дюйма). Механизм курвиметра состоит из обводного колеса,  соединенного системой зубчатых передач со стрелкой. Для измерения длины линии на карте следует предварительно вращением обводного колеса установить стрелку курвиметра на начальное (нулевое) деление шкалы, а затем прокатить обводное колесо строго по измеряемой линии. Полученный отсчет по шкале курвиметра необходимо умножить на величину масштаба карты.

Правильность работы курвиметра проверяют путем  измерения известной длины линии, например расстояния между линиями километровой сетки на карте. Погрешность в измерении линии длиной 50 см  курвиметром составляет не более 0,25 см.

Протяженность маршрута на карте может быть измерена также циркулем-измерителем.

Измеренная по карте длина маршрута всегда будет несколько короче действительной, так как при составлении карт, особенно мелкомасштабных, дороги спрямляют. В холмистой и горной местности, кроме того, имеется значительная разность между горизонтальным проложением маршрута и его действительной длиной из-за подъемов и спусков. По этим причинам в измеренную по карте длину маршрута необходимо вводить поправку. Поправочные коэффициенты для разных типов местности и масштабов карт неодинаковы, приведены в таблице.

Местность	Поправочный коэффициент для карты масштаба
1:50 000	1:100 000	1:200 000	1:500 000
Равнинная Холмистая Горная	1 1,05 1,15	1 1,1 1,2	1,05 1,15 1,25	1,05 1,2 1,3

Из таблицы видно, что в холмистой и горной местности разность между измеренной по карте и действительной протяженностью маршрута значительная. Например, измеренная по карте масштаба 1:100 000 горного района длина маршрута равна 150 км, а действительная длина его будет 150*1.20 = 180 км.

Поправку в длину маршрута можно вводить непосредственно при его измерении по карте циркулем-измерителем, устанавливая «шаг» циркуля-измерителя с учетом поправочного коэффициента.

Измерение площади лекал

Нормирование расхода материалов

Сущностью нормирования является установление рациональной нормы расхода материала на единицу изделия путём разработки рациональной раскладки.

Норма расхода материала – максимально допустимая величина расхода материала для изготовления единицы изделия, установленного уровня качества.

Нормированию подлежат все виды материалов и фурнитуры

Структура нормы состоит из:

1 Полезная площадь лекал с учётом вытачек, но без учета площади припусков на швы надставок и припусков на подгонку рисунка ткани.

2 Технологические потери: межлекальные потери, потери, по ширине учитывая потери от кромки, потери по длине, учитывают потери слабины при настиле, на стык, на равноту конца настила и конечный остаток.

Существует два вида норм:

Индивидуальная – разработанная на единицу изделия для расчета: нормы на раскладку, нормы на настил, нормы расхода ткани на единицу изделия.

Групповая – разработанная на основе лучшей раскладки, применятся для планирования объема продукции.

Очень важным в точном установлении норм является точное измерение площади самих лекал. Существует ряд способов измерения площади лекал. Отмечаем четыре из них.

Геометрический – площадь каждого лекала разбивают на простейшие геометрические фигуры, суммируют их и получают площадь лекал. Погрешность составляет 2–3 %.

Комбинированный (палетка) – заключается в том, что из площади полного прямоугольника, в который вписывается лекало, вычитывают сумму площадей прямоугольников не входящих в форму лекала.

Механизированный – выполняется на машине ИЛ. Она оснащена чувствительным фотоэлементом, её работа основана на базе контактных измерений площади плоских фигур, разной конфигурации путем разложения их на элементы оптической площади.

Способ взвешивания. Лекала раскладывают произвольно на листе бумаге, очерчивают контуры и замеряют площадь прямоугольника, в который вписываются все лекала. Затем прямоугольник отрезают и взвешивают, отдельно вырезают каждое лекало и взвешивают. Дальнейший расчет площади происходит по формуле 6.1:

S_{р –} площадь прямоугольника, см 2 ,

М_р— масса прямоугольника, г

Площади лекал для проектируемой модели представлены в таблице 12.

Таблица 13– Площади лекал. Женское платье спортивного стиля. Размер 164-92-100, вторая полнотная группа, младшая возрастная группа.

Наименование деталей изделия и материалов	Количество единиц, ед.	Площадь, м 2
Лекал	Деталей кроя	Лекал	Деталей кроя
1	2	3	4	5
Основная ткань Трикотажное полотно
1 Середина переда	1	1	0,154224	0,154224
2 Боковая верхняя часть переда	1	2	0,05904	0,11808
3 Боковая нижняя часть переда	1	2	0,054064	0,108128
4 Середина спинки	1	1	0,15808	0,15808
5 Боковая часть спинки	1	2	0,12832	0,25664
6 Рукав	1	2	0,049632	0,099264
7 Воротник	1	1	0,123136	0,123136
8 Обтачка переда	1	1	0,01408	0,01408
9 Обтачка спинки	1	2	0,0064	0,0128
Итого :	9	14	0,746976	1,044432

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Какая погрешность при межевании земли допустима?

Предположим, что владелец земельного участка проводит уточнение границ с целью определения точного метража площади и прохождения границ ЗУ. У него на руках имеется выписка из госкадастра о том, что предельно допустимая величина погрешности для участка площадью 663 м составила 11,6 кв. метров. Межевые работы были проведены в 2002 году, после чего ЗУ занесен в кадастровый реестр.

На момент проведения процедуры уточнения границ нормы предельно допустимых величин изменились. Инженеры провели необходимые замеры на местности, приравненной ко второй категории (земли сельхозназначения): Показатели Описание Разница между площадью ЗУ по документам и фактической площадью, определенной после выполнения геодезических замеров (то есть ∆Р) составила 3,4 м Величина погрешности Mt для данных земель составляет 0,2 м Формула исчисления погрешности выглядит следующим образом: 3,4*0,20*√663=17, 5 кв. м.

Площадь фигуры, её свойства. Способы измерения площадей фигур. Единицы площади. Вычисление площадей квадрата, прямоугольника, треугольника, круга, трапеции.

Первое представление о площадях – в дошк. возрасте (н-р: сравнивая платочки).Геометр фигура плоская, если все точки принадлежат 1 плоскости. S фигуры – положит величина, определяется для каждой фигуры, так что: 1) равные фигуры имеют = S; 2) S фигуры = сумме S всех ее компонентов. Равные фигуры – совпадают при наложении. Равновеликие – S равны. Равносоставленные – две фигуры, которые можно разбить на соответ равные части (только многоугольники). Теорема Бойян и Гервина: 1) равносоставленные фигуры = равновеликие; 2) если у 2 многоугольников S =, то их можно представить из 2 попрано = частей.

Св-ва S: 1)если фигуры =, то = их числ значения S; 2) если фигура состоит из частей, то S = сумме S этих частей; 3) при замене ед S, числ значение S увеличивается во столько раз, во сколько ед S; 4) числ значение S единичного квадрата = 1; 5) если F₁ – часть F₂, то численное значение F₁ 2 2 . Чтобы найти приближенное значение S_(F) достаточно сложить получ числовые значения S по недостатку и по избытку :2. S_(F)

(me+(m+n)e 2 )/2 = ((m+n+m)e 2 )/2= (2m/2 +n/2)e 2 = (m+n/2)e 2 . Для более точно значения – более мелкая палетка, или наклонить с разных углов, и высчитать среднее арифметическое.

Ед S. м 2 , см 2 , дм 2 , км 2 , мм 2 , ар, га, сотка.

Формулы площади квадрата

1) Формула площади квадрата по длине стороны

Площадь квадрата равна квадрату длины его стороны. S = a2

2) Формула площади квадрата по длине диагонали

Площадь квадрата равна половине квадрата длины его диагонали.

где S — Площадь квадрата, a — длина стороны квадрата, d — длина диагонали квадрата.

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон

S = a · b, где S — Площадь прямоугольника, a, b — длины сторон прямоугольника.

Формулы площади треугольника

1) Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты. S = 1 a · h

2) Формула площади треугольника по трем сторонам

Формула Герона: S = √p(p — a)(p — b)(p — c)

3) Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. S = 1 a · b · sin γ

4) Формула площади треугольника по трем сторонам и радиусу описанной окружности.

5) Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. S = p · r, где S — площадь треугольника, a, b, c — длины сторон треугольника, h — высота треугольника, γ — угол между сторонами a и b, r — радиус вписанной окружности, R — радиус описанной окружности,

p = a + b + c — полупериметр треугольника.

Формулы площади круга

1) Формула площади круга через радиус

Площадь круга равна произведению квадрата радиуса на число пи. S = π r2

2) Формула площади круга через диаметр

Площадь круга равна четверти произведения квадрата диаметра на число пи. S = 1 π d2

где S — Площадь круга, r — длина радиуса круга, d — длина диаметра круга.

Формулы площади трапеции

1) Формула Герона для трапеции

S = a + b √(p — a)(p — b)(p — a — c)(p — a — d)

2) Формула площади трапеции по длине основ и высоте

Площадь трапеции равна произведению полусуммы ее оснований на высоту.

где S — площадь трапеции,a, b — длины основ трапеции, c, d — длины боковых сторон трапеции, p = a + b + c + d — полупериметр трапеции.

Источник

Основные способы

Существует три основных способа определения площадей:

При использовании аналитического способа определение площади производится по результатам полевых угловых и линейных измерений (или координат) характерных точек.

Для графического способа используются данные измерений на плане и карте.

Такой способ чаще всего используется при отсутствии информации полевых измерений.

При механическом способе площадь определяется по плану с помощью специального устройства – планиметра.

Иногда используется комбинированный способ определения площади. Например, общая площадь участка определяется по координатам характерных точек аналитическим способом, а площади внутренних участков определяются по плану с помощью графического или механического методов.

Эти три метода имеют различные показатели точности.

Точности других методов, использующих топографическую информацию с планов, зависят еще и от погрешностей приборов, качества плана, масштаба, деформации бумаги.

Аналитический способ

Аналитический способ позволяет по координатам характерных точек границ участка определить его площадь. При этом используются формулы аналитической геометрии.

В соответствии с ними площадь многоугольника S может быть определена по формуле:

• Xi и Yi – координаты i-той характерной точки участка, имеющего вид многоугольника;
• i – порядковый номер характерной точки ЗУ. Этот параметр меняется от 1 до n;
• n – число характерных точек.

Если участок имеет четырехугольную форму, то, в общем случае, для него расчет площади производится по приведенной выше формуле с учетом того, что n=4.

Если участок имеет форму трапеции и известны его стороны, то площадь такого участка можно определить по формуле:

• a и b – основания фигуры;
• h – высота трапеции.

При расчете четырехугольника неправильной формы, когда известны размеры его сторон, вначале определяют величину полупериметра p:

a,b,c,d – величины сторон.

Тогда площадь участка Sу будет равна:

При этом по контуру границ участка производится замер азимута каждой характерной точки. Также определяется расстояние от одной характерной точки до следующей за ней точки. Вся эта информация в дальнейшем вводится в ЭВМ, которая по специальной программе производит расчет площади ЗУ.

Графический метод

При расчете площади участка графическим методом чаще всего изображенный на плане участок сложной формы делят на участки элементарного вида (треугольники, прямоугольники, трапеции), затем вычисляют и суммируют площади этих фигур.

Точность графического метода зависит от точности графического измерения на плане. Известно, что точность измерения с помощью циркуля постоянна и равна 0,1 мм. Поэтому относительная ошибка при измерении коротких линий больше, чем при измерении длинных линий. В связи с этим желательно, чтобы простые фигуры были больших размеров и с близкими по размерам основаниями и высотами.

Такой метод удобен в случае, когда имеется небольшое количество характерных точек. В противном случае целесообразнее определять площадь участка по координатам точек, измеренных на плане.

Палетка представляет собой прозрачный лист, на который нанесены деления. Этот лист накладывается на план участка. Сосчитав количество делений, входящих в контур участка, и определив площадь одного деления с учетом масштаба, можно оценить площадь участка.