Площадь четырехугольника

Информация

При строительстве или ремонте жилого помещения важнейшим вопросом является его обогрев. Расчет эффективной системы отопления – ответственная задача для строителя-теплотехника. Однако, можно самостоятельно сделать расчет радиаторов отопления по площади помещения с помощью онлайн калькулятора. Необходимо только ввести известные данные в программу.

Функции калькулятора

Калькулятор для расчета радиаторов отопления на квадратный метр или по мощности секций является онлайн программой и состоит из:

• блока окон «Вид радиатора»;
• десяти строк ввода данных;
• блока окон «Тип подключения»;
• четырех строк с выводом готовых расчетов.

Программа произведет расчет количества секций радиаторов отопления; тепловых потерь помещения; удельных теплопотерь помещения; количества тепла, выделяемого одной секцией. Всю полученную информацию можно сохранить в файле PDF или вывести на печать.

Принцип работы на калькуляторе

Для получения готовых расчетов следуйте нижеуказанному алгоритму:

Выберете необходимый вид радиатора. В строке ниже автоматически появится мощность одной секции выбранного вида радиатора, в ваттах.
В строках 2-4 укажите размеры комнаты: длину, ширину, высоту в метрах.
Выберете качество остекления.
Выберете площадь остекления (равна отношению площади окна к площади помещения), в %.
Укажите степень утепления.
Выберете климатическую зону – регион проживания.
Укажите количество внешних углов и стен комнаты.
Выберете вариант помещения, которое находится над комнатой.
Укажите температуру теплоносителя, в ℃

Это очень важно, например центральное отопление дает 70-80 градусов, а котел на твердом топливе если есть дома тёплый пол настраивают на 50-60
Выберете планируемый тип подключения.

После этого появится следующая информация:

• Количество секций, в штуках.
• Тепловые потери помещения, в ваттах.
• Удельные теплопотери помещения, в Вт/м2.
• Количество тепла, выделяемого 1 секцией, в ваттах.

Полезная информация

Важнейшими техническими характеристиками различных моделей радиаторов отопления являются:

• Мощность секций радиатора. Чем больше мощность радиатора, тем выше теплоотдача и эффективность отопительного прибора.
• Рабочее давление радиатора. Высокий порог данного параметра позволяет выдерживать гидравлические удары и перепады давления в системе, увеличивает срок службы изделия.
• Материал и вес радиатора. Вид материала (металла, сплава) напрямую влияет на прочность и долговечность отопительного прибора, его коррозионную стойкость. Вес изделия важен при монтаже, особенно, если устанавливать радиаторы будет один человек.

На рынке радиаторов отопления присутствуют четыре основных вида: стальные, чугунные, алюминиевые и биметаллические радиаторы.

Стальные радиаторы – имеют хорошую теплоотдачу и относительно невысокую стоимость. Однако, они не достаточно устойчивы к гидроударам и высокому давлению, подвержены коррозии. Различают панельные и трубчатые радиаторы из стали.

Чугунные радиаторы – самый популярный и долговечный вид радиаторов в России для централизованного отопления. Обладают отличной теплоотдачей, стойкостью к коррозии и гидроударам. В то же время, радиаторы из чугуна долго нагреваются и долго остывают; имеют большой вес, что является недостатком при монтаже одним специалистом.

Алюминиевые радиаторы – одни из самых популярных современных видов радиаторов. Изготавливают литые и экструзионные радиаторы из алюминия

Отличаются высокой теплоотдачей и небольшим весом, что важно при установке приборов. При этом, они чувствительны к гидроударам и перепадам давления в системе отопления, быстро нагреваются и быстро остывают

Биметаллические радиаторы – обладают относительно лучшими характеристиками среди всех видов радиаторов. Изготавливаются из двух материалов: внешней алюминиевой оболочки и внутренних стальных или медных труб. Обладают высокой теплоотдачей и прочностью, хорошей стойкостью к коррозии и гидроударам, имеют сравнительно небольшой вес.

Справка

Радиатор отопления – отопительный прибор, конструктивно состоящий из отдельных элементов трубчатого или вытянутого вида – секций, с внутренними каналами, по которым циркулирует теплоноситель, как правило, вода. Тепло от радиатора отопления отводится конвекцией, излучением и теплопроводностью.

Как определить площадь стен?

Умение производить расчет площади стен, является очень важным. Зная эту величину, вы сможете высчитать необходимое количество кирпичной кладки, краски, шпатлевки, обоев и других материалов, которые могут пригодиться для строительства и ремонта. Здесь также нет абсолютно ничего сложного.

Чтобы высчитать квадратуру комнаты, необходимо вымерить ее высоту, длину и ширину. Дальше все зависит от того, какой именно является измеряемая вами стена – глухой, или с проемами.

Сплошная стена

Если стена глухая (то есть дверь и окна – в другой комнате), все дальнейшие вычисления выполняются по формуле:

Напомним, что для вычисления периметра, нужно сложить длину и ширину комнаты:

Как измерять стены с дверью и окном?

Если в комнате есть окно или дверь, то для получения актуальных показателей их необходимо обязательно измерить. Воспользовавшись все той же рулеткой, узнайте высоту и ширину оконного проема, умножьте один результат на другой и вычтите это произведение из общей площади. Не надейтесь на то, что их форма является правильной.

Приведем пару примеров.

Пример 1. Стена с дверным проемом:

• Общая S стены – 2,7 м х 8,0 м = 21,6 м2;
• S дверного проема в стене – 2,3 м х 0,9 м = 2,07 м2;
• S стены без дверей – 21,6 м2 – 2,07 м2 = 19,53 м2.

Пример 2. Стена с оконным проемом:

• Общая S стены – 2,4 м х 5 м = 12 м2;
• Площадь окна – 1,4 м х 1,65 м = 2,24 м2;
• S стены без окна – 12 м2 – 2,24 м2 = 9,76 м2.

Как посчитать площадь окна

Для многоквартирных многоэтажных домов, а также для типовых проектов индивидуального строительства площадь окна в жилой комнате – параметр, просчитанный специалистами заранее, и для владельца квартиры он не имеет значения, так как уже соответствует всем нормам и стандартам. Но для застройщиков, которые возводят собственное жилье с «нуля», по собственному проекту, площадь окна – такой же важный параметр, как марка цемента или прочность бетона. Расчетная площадь остекления помогает не только сделать правильное освещение в помещении – это и правильная расстановка мебели, и правильные расчеты балки перекрытия проема, и многое другое.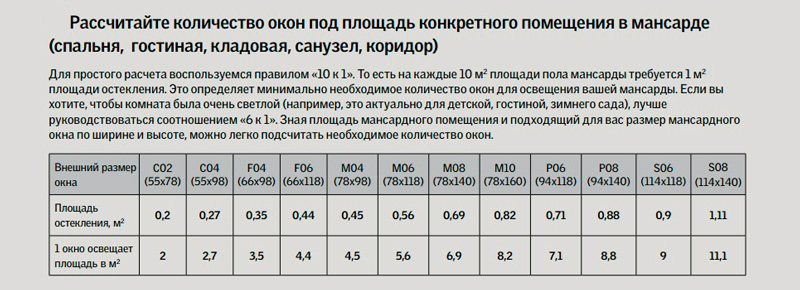

Пошаговый расчет площади комнаты

Шаг 1. Первым делом необходимо приготовить все измерительные инструменты, а также листок и ручку. На бумаге можно предварительно начертить схему комнаты, стараясь максимально сохранить геометрию и отобразить все ниши и детали помещения. Рулетка используется максимально длинная.

Подготовка всего необходимого

Шаг 2. Измеряется длина комнаты. Если она настолько велика, что рулетки не хватает, то замеры снимаются поэтапно. Для начала производится замер на максимальную длину рулетки, в месте ее окончания делается отметка, от которой потом снова производится замер до конца комнаты.

Для начала нужно измерить длину комнаты

Шаг 3. Измеряется ширина комнаты (вдоль стены с меньшей длиной). Рулетка располагается под прямым углом к ранее измеряемой стене комнаты (длине). Полученные данные записываются.

Измеряется ширина комнаты

Шаг 4. Полученные показатели перемножаются между собой. Для этих целей рекомендуется использовать калькулятор. При необходимости значение площади округляется в большую сторону.

Полученная цифра округляется в большую сторону

Шаг 5. Если необходимо измерить площадь сложной геометрически комнаты, то для начала сложная фигура делится на несколько простых – квадратов, треугольников, прямоугольников. Объект изображается на листочке бумаги схематически, схематически делится.

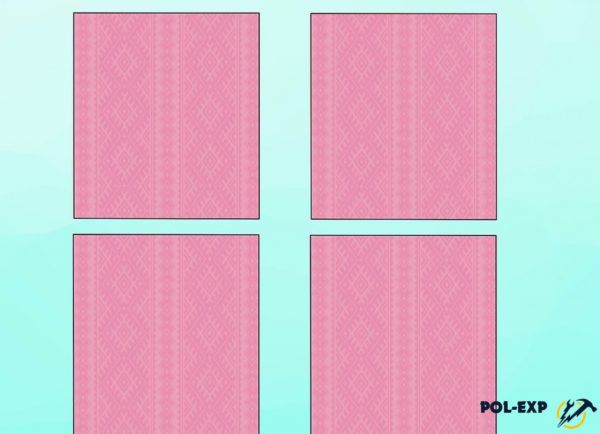
Комната разделена на 4 прямоугольника

Шаг 6. Производится замер каждой фигуры в отдельности. Например, прямоугольники, треугольники.

Каждая фигура замеряется отдельно

Шаг 7. Производится вычисление площади каждой фигуры. Далее все полученные значения суммируются и получается полная точная площадь пола комнаты.

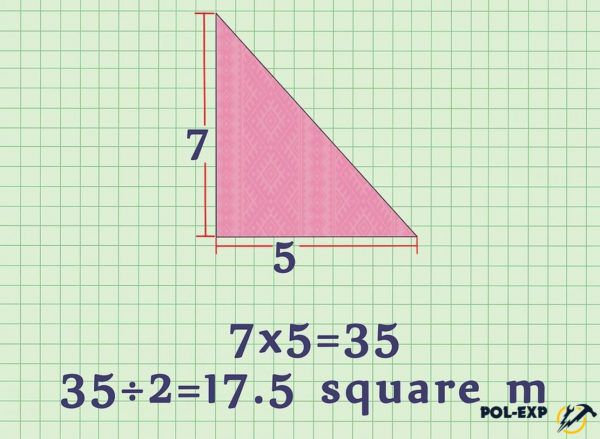
Пример расчета площади треугольника

Помещения с неправильными очертаниями

Как найти площадь помещения неправильной формы? Его необходимо разбить на те фигуры, из которых состоит все помещение. Например, прямоугольник с полукругом (если это комната с эркером), два прямоугольника (помещение с нишей), несколько треугольников и т.п. Их прорисовывают на бумаге для большей наглядности, проставляют полученные замеры и высчитывают по формулам.

Расчет площади треугольника

Разбивая площадь комнаты на несколько геометрических фигур, будьте внимательны с треугольниками. Лучше делать это так, чтобы они были прямоугольными, это упростит расчеты. Иначе будет большая вероятность возникновения погрешностей.

Расчет площади круга

Иногда в помещениях имеются круглые выступы, сегменты, полукружья, секторы. Или же вся комната округлой формы. В этом случае пригодится формула расчета площади круга: S=πR2. Для этой формулы требуется величина радиуса: замерьте расстояние от виртуального центра до края дуги или разделите диаметр на 2.

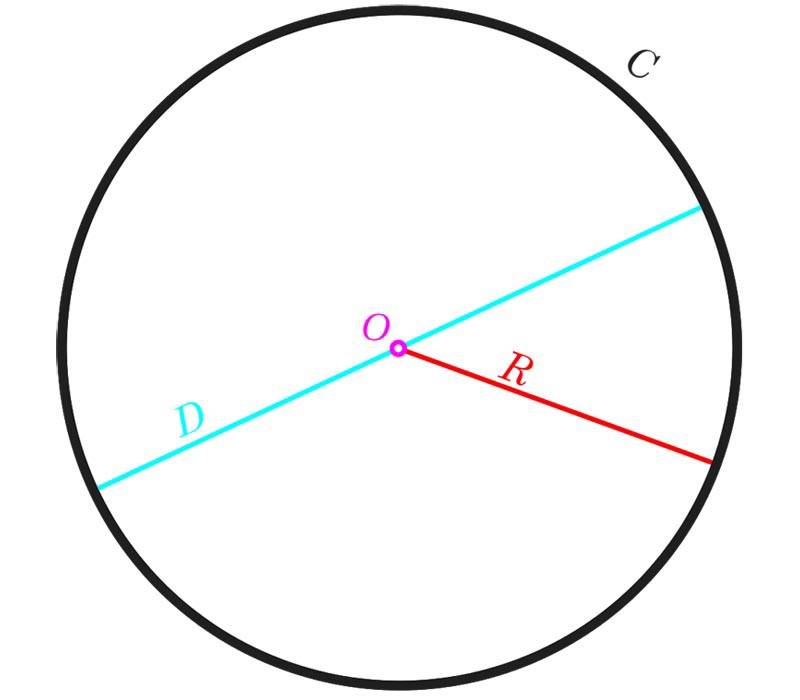
Площадь сегмента высчитывается по следующей формуле:

Расчет площади трапеции

У трапеции две параллельные стороны и две – не параллельные. Исходя из этого рассчитать площадь трапеции можно несколькими путями:

• разделить трапецию на прямоугольники и треугольники и просчитать площадь каждой полученной фигуры, затем просуммировав составляющие;
• воспользоваться формулой: S= (a+b)*h/2, в которой a и b –параллельные стороны, а h – высота (расстояние между сторонами). Высоту лучше замерить в нескольких точках для надежности.

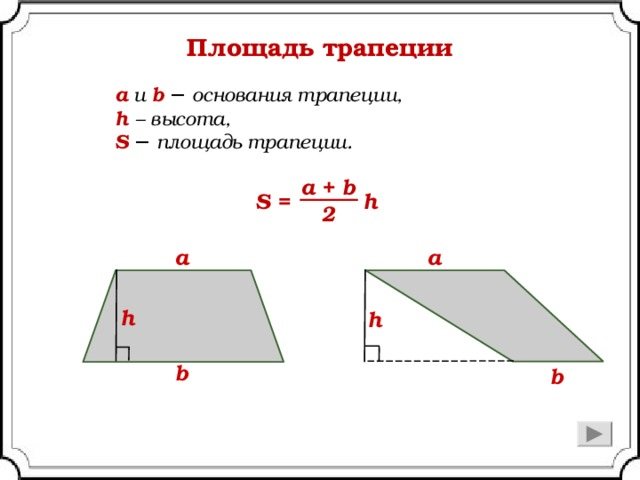
Правильный результат получится вследствие точных замеров.

Площадь стен со сложной поверхностью

Нередко в помещениях много разных элементов, которые усложняют подсчет площади. Так что если стены не прямоугольные или есть разные дополнительные детали, необходимо воспользоваться иным способом расчета площади дома.

1. Площадь стен дома с вычетом дверей и окон.

Двери и окна обычно вычитают из общей площади, потому что на них не идет расход материала. Но как посчитать площадь стен без них?

Для начала замеряется ширина и высота окон и дверей.

Формула для площади поверхности – S = a x h.

Если ширина окна 1 м, а высота 1,5 м, то S = 1 х 1,5 = 1,5 м².  При ширине двери 0,9 м и высоте в 2 м получаем S = 0,9 х 2 = 1,8 м². Теперь нужно отнять от общей площади, площадь окон, дверей и получается площадь без них. То есть,

S стен = 66 – 1,5 – 1,8 = 62,7 м² (если использовать площадь стен, полученную в предыдущем пункте).

1. Если комната нестандартной конструкции.

Когда помещение имеет нестандартную форму, расчет площади стен проводится немного иначе. Сначала считается площадь каждой стены в отдельности.

S = a x b, где, а – ширина стены, b – высота стены.

Если есть колонны, выступы, их площадь также измеряется, а затем все эти площади суммируются. То есть, итоговая формула это S = S1 + S2 + S3 + S4 и т. д.

Важно!
В редких случаях геометрические параметры стен абсолютно правильные. Так что для наиболее точных расчетов стоит делать измерения в нескольких местах, а потом выводить среднее арифметическое число и уже его использовать в формулах.

1. Если имеются круглые элементы в архитектуре.

Помещения с круглыми или полукруглыми стенами это не редкость. Чтобы просчитать их площадь используется другая формула. Первым делом вымеряется их периметр. Для этого нужно умножить диаметр на 3,14 (число Пи, π). А затем уже подсчитывается и площадь по формуле:

S = P x h, где, h – это высота.

Когда нужно вычесть из общей квадратуры площадь круглых объектов, нужно рассчитать площадь круглых поверхностей и просто отнять их. Но, если нет возможности вымерять диаметр или радиус, то вымеряют длину окружности (P) и считают площадь, применяя формулу S = P² / 4 π.

1. Площадь с треугольными элементами.

Треугольные стены могут быть, к примеру, на чердаке или в случае, когда используются сложные конструкции на потолке или архитектурные украшения на стенах. В зависимости от типа треугольника использовать можно разные формулы.

• Разносторонний треугольник: S = , где, а – основа треугольника – нижняя сторона, а h – высота от пола к верхнему углу.
• Прямоугольный треугольник: S = , где, а – высота треугольника, а b – нижняя, горизонтальная сторона.
• Равносторонний треугольник (правильный): S = , где, а – сторона треугольника.

Информация о прямоугольнике

Прямоугольник — четырехугольная геометрическая фигура, противолежащие стороны которой равны и углы являются прямыми. Частным случаем данной фигуры считается квадрат. У него все углы прямые, а также все стороны равны между собой. Для выполнения расчетов нужно знать основные соотношения, свойства и признаки.

Важным аспектом является идентификация фигуры и применение к ней формул и соотношений. В двухмерной геометрии, которую еще называют эвклидовой, можно встретить необычный признак, позволяющий определить принадлежность четырехугольника к прямоугольнику. Его формулировка следующая: достаточно хотя бы трех углов, равных 90 градусам, чтобы четырехугольник считался прямоугольником.

Утверждение легко доказывается. Это связано с тем, что по теореме о сумме внутренних углов произвольного четырехугольника, составляющей 360 градусов, четвертый угол тоже равен 90. Нужно выполнить следующие расчеты для определения градусной меры четвертого угла: D = 360 — (90 + 90 + 90) = 90. Необходимо отметить, что смежные с ними углы равны 90.

Свойства и признаки

Очень часто новички путают свойства и признаки фигуры. Однако это совсем различные понятия. Признаками фигуры называются характерные особенности, которые позволяют отнести ее к тому или иному классу. Свойства — совокупность аксиом, позволяющих использовать некоторые данные при решении или доказательстве теорем и тождеств. Прямоугольник обладает следующими признаками:

1. Условие параллельности и равенства противоположных сторон.
2. Наличие четырех прямых углов.
3. Равенство диагоналей.
4. Квадрат диагонали равен суммарному значению квадратов двух сторон, которые не противоположны.
5. Все стороны не равны между собой.

Очень важно уметь различать геометрические фигуры. Поскольку прямоугольник является параллелограммом, то их часто путают

Основное его отличие — это равенство всех углов 90 градусов. У параллелограмма и ромба углы будут равняться 90 в том случае, когда они являются квадратами. Последний отличается от искомой фигуры (прямоугольника) равенством всех сторон. Поскольку прямоугольник является частным случаем параллелограмма, то обладает такими же свойствами:

1. Углы равны между собой 90 градусов.
2. Противолежащие параллельные стороны равны.
3. Сумма всех внутренних углов составляет 360.
4. Диагональ, проведенная внутри прямоугольника, делит его на два равнозначных треугольника, которые являются равновеликими. Они равны по третьему признаку равенства треугольников (размерности сторон одной фигуры равны значениям сторон другой фигуры).
5. Треугольники, полученные при проведении двух диагоналей, равны по всем признакам (углам и сторонам).
6. Диагонали пересекаются между собой в точке, которая делит их на четыре равные части.
7. Точка пересечения диагоналей — центр симметрии.
8. Сумма квадратов двух диагоналей соответствует суммарному значению квадратов всех сторон фигуры.

Периметр и размерность

Нужно ввести некоторые обозначения. Пусть стороны прямоугольника АВСД обозначаются литерами a и b. Поскольку диагонали равны, то можно только обозначить размерность одной буквой «d». Периметром называется сумма всех сторон заданной фигуры. Он обозначается литерой P. Для его нахождения применяется формула такого вида: P = 2 * (a + b). Однако бывает случай, когда известна только одна его сторона и диагональ. Формула приобретает следующий вид: P = 2a + ^(1/2) и P = 2b + ^(1/2).

Чтобы вычислить площадь прямоугольника, следует воспользоваться таким соотношением: S = a * b. Эта базовая формула, которая используется также в строительной сфере и физике. Однако существует еще один способ, с помощью которого можно узнать площадь прямоугольника. Она находится с помощью формулы Герона для треугольников с площадями S1 и S2, а затем результат умножается на 2. Эта особенность основывается на свойстве фигуры, поскольку диагональ делит его на два равных треугольника.

Соотношение имеет следующий вид: S = S1 + S2 = 2S1= 2 * ^(1/2). Переменная «p» — полупериметр треугольника. Он находится таким методом: p = P / 2 = (a + b + d) / 2.

Уточняющий расчет

Однако, это не единственные ориентиры для проведения расчетов размеров окон. Есть и другие вполне рабочие методы определения площади световых проемов по специальным формулам, в которых один из важнейших параметров — также площадь пола.

Но найденные по таблицам или формулам значения площади остекления все же являются ориентировочными. Обязательно должен производиться уточняющий расчет естественной освещенности помещений.

На сегодняшний день в разных странах используют несколько различных методов расчета КЕО (коэффициента естественного освещения):

• метод транспортиров
• метод сеток
• метод лучей
• метод коэффициента использования светового потока
• аналитические методы

Все они дают близкие по значениям результаты.

Как посчитать приблизительный размер окна в квартире или доме

Еще на стадии проектирования определяются все параметры оптимального остекления для каждого конкретного помещения. Расчеты достаточно сложные для неспециалиста, поэтому рассмотрим их результаты для одной жилой комнаты при угле падения дневного света от 18 до 30 градусов.

Для комфортного освещения отношение площади остекления к площади пола этого помещения должно составить от 1/8 до 1/5. Это значит, что окно займет площадь 14–17% от площади пола.

Угол падения солнечных лучей зависит от этажности и наличия соседних домов. Чем ближе стоят дома-соседи и чем они выше, тем больше этот угол, а значит, тем меньше освещенность Вашей комнаты. Возможно, ее придется компенсировать большими размерами окна.

Что касается высоты подоконника, то она определяется назначением помещения:

• в жилых комнатах — от 70 до 90 см;
• в рабочих помещениях — от 90 до 100 см;
• в кухне — 125 см;
• в санузлах и подсобках — от 130 до 150 см;
• в гардеробных — 175 см.

Как посчитать площадь комнаты в квадратных метрах

Рассчитать площадь комнаты, часто надо при закупке материалов для строительства или ремонта. Например, некоторые виды напольного покрытия продают на квадраты (то есть, на квадратные метры). Чтобы правильно рассчитать его количество, надо знать площадь пола (часто говорят квадратура комнаты, что по сути одно и то же).

Можно найти площадь комнаты зная длину и ширину

Измерения

Берем рулетку, листок бумаги, карандаш и калькулятор. На бумаге рисуем план комнаты. При помощи рулетки измеряем длины всех стен. Измерения проводим на уровне пола — если постройка старая, велика вероятность того, что стены «завалены» в ту или другую сторону. Тем более что определяем площадь пола, так что логичнее измерять вплотную к стенам, но мерную ленту тянуть по полу.

Схема комнаты с нанесенными измерениями

На схеме проставляем измерения. Лучше всего в метрах. Точность измерений — до сантиметра. Это понадобится при покупке материалов, которые продаются на погонные метры — линолеум, ковролин или другие рулонные покрытия. Чтобы посчитать площадь комнаты в квадратных метрах, тоже желательна такая точность. Хоть можно, конечно, и округлить. Но лучше это сделать уже получив результат.

Как высчитать квадратуру комнаты

Имея длину и ширину комнаты прямоугольной формы, цифры надо просто перемножить. На рисунке выше такая комната нарисована справа. Длинная стена равна 7 м, короткая — 4 метрам. Перемножаем 7*4 = 28 квадратных метров. Это и есть площадь этого помещения, пола. Другими словами, мы нашли квадратуру. Используя эту цифру, можно покупать напольное покрытие. Но надо иметь в виду, что требуется некоторый запас — на подгонку, подрезку. Чем сложнее схема укладки и чем больше фрагменты напольного покрытия, тем запас должен быть больше.

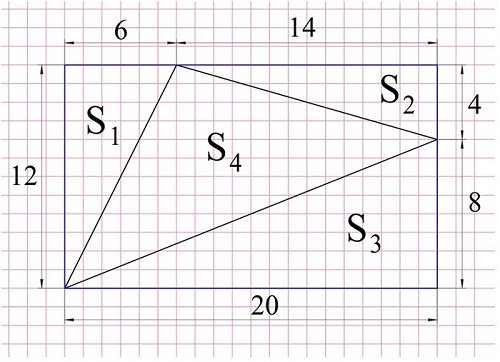
Часто комната не прямоугольная, а имеет более сложную форму. Чтобы посчитать площадь такой комнаты в квадратных метрах, ее разбивают на простые фигуры. Если удается — на прямоугольники или квадраты. Например, Г-образную комнату разбивают на два прямоугольника. Затем считают площадь каждого прямоугольника отдельно, потом их складывают.

Как найти площадь комнаты сложной формы

• Считаем большой прямоугольник: 5 м * 4,35 м = 21,75 м².
• Находим квадратуру маленького: 2,5 м * 2,65 м = 6,625 м².
• Площадь пола в этом помещении равна сумме 21,75 м² + 6,625 м² = 28,375 м².

При покупке материалов, проще пользоваться округленными значениями. Чаще всего говорят, что в этом помещении 28,4 квадрата.

Если помещение имеет участок «срезанной» стены, как на рисунке ниже, проще всего дорисовать прямоугольник так, чтобы косая делила его на два треугольника. В этом случае снова-таки получаем Г-образную комнату. Как высчитать ее площадь уже знаем.

Получается, ищем площадь трех прямоугольников

А недостающий участок — это половина маленького прямоугольника. То есть, находим площадь этого маленького прямоугольника, делим ее пополам и прибавляем к размерам Г-образного участка.

Приведем пример расчета подставляя произвольные значения:

• Большой прямоугольник: 1,75 м *1,93 м = 3,3775 м². Для простоты округлим до 3,38 м².
• Средний прямоугольник: 1,18 м * 0,57 м = 0,6726 м².  Снова округлим до 0,67 м².
• Самый маленький прямоугольник (в нашем случае это будет квадрат): 0,57 м *0,57 м = 0,3249 м2, после округления имеем 0,33 м².
• Чтобы найти общую площадь складываем квадратуру двух прямоугольников и добавляем половину площади последнего, самого маленького участка. 3,38 + 0,67 +0,33/2 = 3,38 + 0,67 +0,17 = 4,22 м².

Такая методика — разбиение на простые фигуры — самый удобный и простой метод. Всегда стоит стараться преобразовать сложную фигуру в набор простых. Правда, измерений может потребоваться больше.

https://youtube.com/watch?v=YL07nZH5ueY

Формулы

 

Дан прямоугольник ABCD.

Периметр равен сумме длин сторон.

P_ABCD = AB + BC + CD + AD

Противоположные стороны прямоугольника равны.

P_ABCD = 2 * AB + 2 * BC = 2 * (AB + BC)

Следовательно, для того, чтобы высчитать периметр прямоугольника, нужно сложить длины двух сторон и умножить результат на 2.

У квадрата все стороны равны.

Поэтому, периметр квадрата равен:

  P_ABCD= 4 * AB

Площадь прямоугольника равна произведению длины на ширину.

  S_ABCD = AB * BC

Определить площадь, периметр, объем, длину, диаметр, высоту и остальные геометрические величины поможет онлайн-калькулятор https://max-calc.ru.

На сайте вы сможете не только получить готовое решение, но и посмотреть всю необходимую справочную информацию.

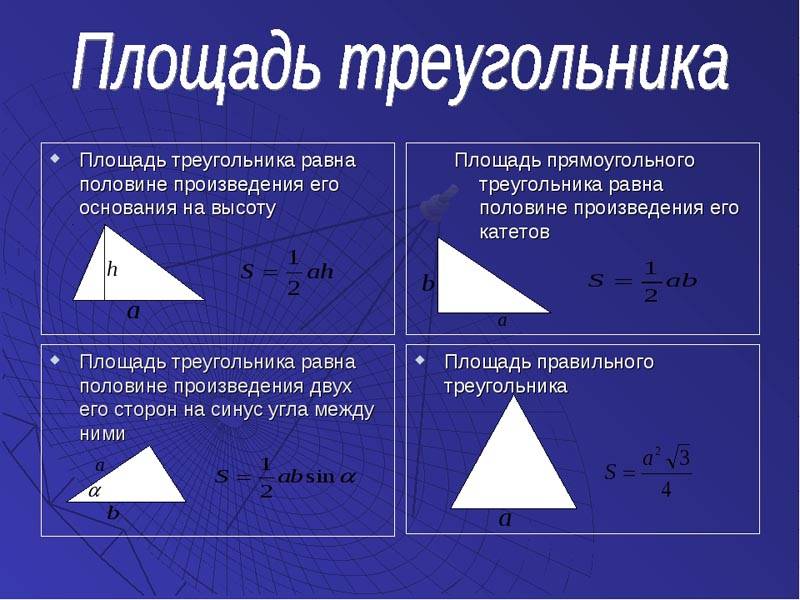
Площадь прямоугольного треугольника

Пусть в прямоугольном треугольнике известны два его катета. Обозначим их буквами а и b. Как тогда вычислить площадь такого треуг-ка?

Прямоугольный треугольник можно достроить до прямоугольника:

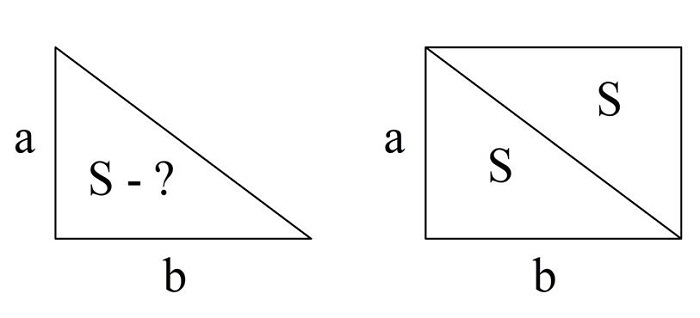
Площадь получившегося прямоугольника равна произведению чисел а и b. С другой стороны, прямоугольник состоит из двух треуг-ков площадью S, поэтому его общая площадь составляет 2S. Тогда можно записать, что

Задание. Катеты прямоугольного треугольника имеют длины 3 и 4. Определите его площадь.

Решение. Просто подставляем в формулу вместе букв a и b числа 3 и 4:

Задание. Площадь прямоугольного треугольника равна 100, а один катет больше другого вдвое. Найдите оба катета.

Решение. Пусть меньший катет равен х, тогда больший катет будет равен 2х. Выразим площадь прямоугольного треугольника через х:

Естественно, нас интересует только положительный корень, а отрицательный можно отбросить:

x = 10

Меньший катет оказался равным 10, тогда больший катет, который вдвое больше, будет равен 20.

Ответ: 10; 20.

Задание. Найдите площадь фигуры, показанной на рисунке. Сторона каждой клеточки имеет длину, равную единице:

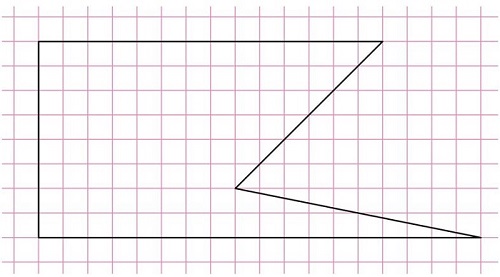
Решение. Эту фигуру можно разбить на квадрат со стороной 8 и два прямоугольных треуг-ка, то есть всего на три фигуры:

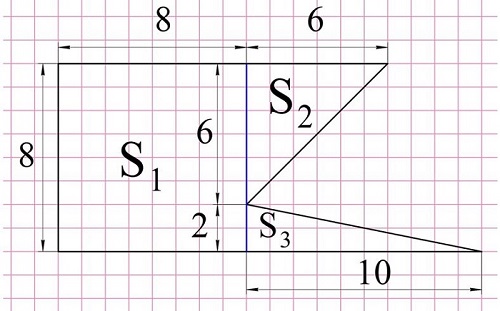
Подсчитаем площадь каждой из трех фигур по отдельности:

Чтобы найти площадь всей фигуры, достаточно просто сложить три полученных числа:

Задание. Вычислите площадь треуг-ка, изображенного на рисунке (площадь каждой отдельной клеточки составляет единицу):

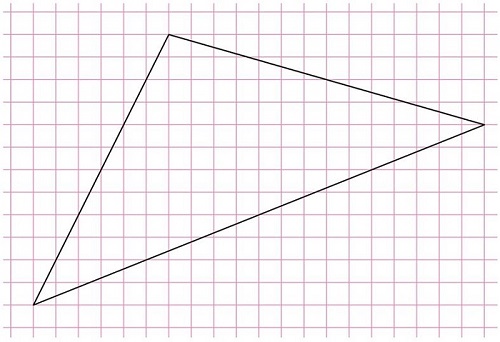
Решение. Здесь проблема заключается в том, что треуг-к прямоугольным не является. Однако можно построить прямоуг-к, который будет состоять сразу из 4 треуг-ков:

Мы можем найти как площадь всего прямоугольника (обозначим ее как S), так и площади трех прямоугольных треуг-ков S₁, S₂ и S₃:

Как рассчитать квадратуру стен

Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:

• высота потолков;
• высота и ширина дверных проемов;
• высота и ширина оконных проемов.

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.

Удобнее всего размеры наносить на план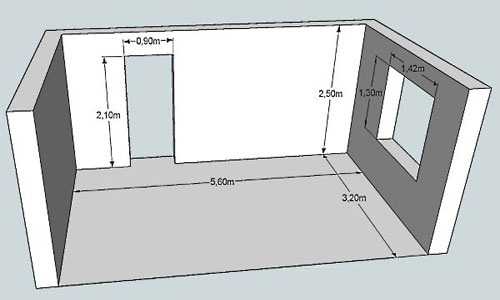

Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.

1. Стена с дверью:
   • 2,5 м * 5,6 м = 14 м². — общая площадь длинной стены
   • сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 м².
   • стена без учета дверного проема — 14 кв.м — 1,89 м² = 12,11 м²
2. Стена с окном:
   1. квадратура маленьких стен: 2,5 м * 3,2 м = 8 м².
   2. сколько занимает окно: 1,3 м * 1,42 м = 1,846 м², округляем, получаем 1,75 м².
   3. стена без оконного проема: 8 кв. м — 1,75 м² = 6,25 м².

Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 м² + 12,11 м². + 8 м² + 6,25 м². = 40,36 м².

Общие рекомендации

Для получения точных цифр строители рекомендуют измерять стену в трёх местах (в начале, середине и в конце). После чего полученные данные стоит суммировать и разделить на 3 и таким образом высчитать среднее арифметическое. Подобная процедура помогает избежать погрешности, даже если стены не самые ровные.

При измерении оконных и дверных проёмов не стоит рассчитывать правильность их формы.

Измерение проёма окна

Лучше собственноручно перемерить все четыре стороны, а не только две соприкасающиеся. Такой подход обезопасит вас от последствий халатности строителей и лишних затрат (например, при замене окон или дверей).

Каковой бы не была причина, по которой вы всё же решили выяснить, как самостоятельно посчитать площадь помещения — помните, что любую работу желательно делать качественно. Поэтому постарайтесь тщательно спланировать весь процесс, подготовьте необходимые инструменты, и смело приступайте к проведению замеров и вычислениям. А наши советы, надеемся, смогут облегчить вам их выполнение.

Вычисление площади прямоугольной комнаты

Помещение, не имеющее никаких, даже небольших, выступов и ниш или, попросту говоря, прямоугольное – самый простой вариант для снятия мерок и подсчета значений площади. Здесь достаточно вспомнить самую простую формулу из курса математики – как рассчитывается площадь такой фигуры, как прямоугольник. Для этого необходимо измерить лишь ширину (А) и длину комнаты (B). Таким образом, мы получаем, что S (площадь) будет равна значению, которое будет получено в результате перемножения двух показателей А и В.

Расчет площади прямоугольной комнаты

Результаты всех измерений указываются в метрах. После запятой указываются сантиметры. Например, длина стены получилась 376 см, тогда получается (в 1 м – 100 см), что длина этой стены будет равна 3 м 76 см.

Меряем прямоугольный пол

Если в комнате есть камин, то нужно посчитать его площадь и отнять от получившейся цифры. Ведь под камином напольное покрытие укладываться не будет. Конечно, если речь не идет о демонтаже этого сооружения.

Как высчитать метр квадратный: единицы изменения

При расчете площадей потолка, пола и стен, необходимо выяснить, как рассчитать квадратный метр. Для вычислений необходимо выбрать мерную ленту или рулетку с нанесением делений в сантиметрах или метрах. Такое приспособление применяются для площади в квадратных метрах.

Если величина получается больше метра, то используются не только метры, но и сантиметры.

Чтобы правильно провести расчеты можно воспользоваться калькулятором квадратных метров. При необходимости померить всю длину, можно делать это поэтапно. Например, сделать отметку там, где закончилась рулетка, а затем протянуть ее еще раз.

В таблице представлены распространенные единицы измерения площади

Ширина меряется также рулеткой. При этом ее располагают под углом в 90 градусов к длине. Если длина меньше метра, то необходимо округлить в сторону ближайшего сантиметра.

При расчете квадратных метров калькулятором, не всегда получается выполнить измерения в метрах. Показатель отображается, как в метрах, так и в сантиметрах. При этом 1 см равняется 0,01 метра. Например, 98 см равно 0,98 м. То есть можно записать 2,98 м. Чтобы получить площадь нужно длину умножить на ширину. Округлять значение можно в большую сторону.

В таблице перевода величин можно узнать необходимые значения

Стоит отметить и другие единицы измерения:

• в 1 квадратном фунте – 0,093 квадратных метра;
• в ярде – 0,84 кв. м.

Умение правильно посчитать площадь необходимо в таких случаях:

требуется точный расчет материалов для ремонта;
наемные мастера часто проводят расчеты оплаты за квадратный метр, что необходимо перепроверять для исключения обмана;
необходимы знания расчетов при выборе площади

Часто оплата коммунальных услуг вычисляется, исходя из размеров комнаты;
чтобы определить нормативы освещенности также нужно знать габариты помещения;
зная площадь, всегда можно посчитать объем, что очень важно при установке отопительных, вентиляционных и климатических устройств.. Значения для погонного метра

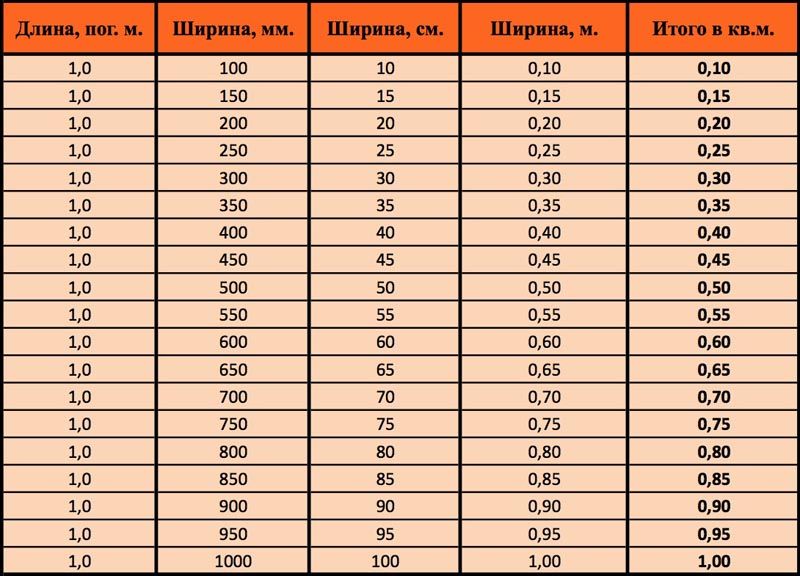Значения для погонного метра

В ролике дается простое объяснение необходимых значений:

Watch this video on YouTube

Основные типы крыш и их достоинства

Формы крыш для дома.

Перед тем как делать крышу, нужно определиться, какие материалы будут использоваться для кровельного покрытия, теплоизоляции, гидроизоляции и так далее. Нужно составить точный план, на котором будут нанесены все размеры, желательно, чтобы все было в цифровых значениях. Знать площадь необязательно, это нужно, чтобы точно рассчитать количество материала для строительства и не переплачивать. После того как собраны все сведения, застройщик может начинать устанавливать крышу для дома.

Любой специалист в этой области должен знать, какие типы их существуют. Они бывают односкатные, двухскатные, трехскатные, вальмовые, полувальмовые, щипцовые и многоскатные. Наиболее просто можно посчитать те из них, которые не имеют изломов. Но все чаще строители делают многоскатные и вальмовые кровли, поэтому материал приходится тщательно подсчитывать. Если в простых крышах все поверхности представлены в виде правильных треугольников или трапеций, то в последнем случае они могут иметь самые различные геометрические фигуры.

Как высчитать площадь комнаты

Для этого нужны лишь минимальные знания из школьной математики. Все помнят, что площадь прямоугольника равна его длине, умноженной с помощью калькулятора на ширину. Этим правилом нужно пользоваться при замере полов и стен в прямоугольных или квадратных помещениях, например, ванной комнаты. Можно записать формулу:

S = A*B, где S — это искомая нами квадратура помещения, а A и B — длина и ширина.

Но даже в такой простой формуле нужно себя перепроверить. Мало в каких домах стены и полы идеально ровные. Для того чтобы не ошибиться при покупке материалов, нужно измерить комнату не только по углам, но еще и проверить высоту или ширину посередине комнаты. Если эти значения будут отличаться от предыдущих замеров в большую сторону, то использовать при подсчете нужно именно их, чтобы взять материалы с небольшим запасом. Пусть лучше немного останется, чем закончится в самый последний момент, когда ремонт уже будет подходить к концу.

Измерение площади стен с окнами и дверьми

Нужно измерить площадь, которую занимают окна и двери. Для этого таким же образом замеряем и записываем их длину и ширину и высчитываем их квадратуру. В итоге от общей квадратуры стены отнимаем на калькуляторе полученные величины для проемов и получаем нужную цифру.

Например, площадь стен в комнате равна 36 квадратных метров. После измерения окна выяснили, что его размеры равны 4 метрам квадратным. Значит, материалы для отделки комнаты нужно покупать с расчетом на 32 квадратных метра.

Измерение комнаты с нишами

В том случае, если комната имеет неправильную форму, в ней есть выступы, ниши или предметы мебели, которые нельзя переместить, то для расчета площади используется принцип, аналогичный расчету площади комнаты с окнами. Разные ниши могут влиять на площадь стен и пола. Для правильного расчета нужно измерить в отдельности площадь каждого такого элемента и вычесть ее из общей квадратуры нужной нам поверхности: таким же образом вычитаем на калькуляторе площадь маленьких прямоугольников из большого.

Измерение площади комнаты неправильной формы

Периметр помещения измерить просто. Это сумма длин всех его сторон. Для этого достаточно пройтись с рулеткой вдоль всех стен и суммировать полученные отрезки.

Теперь, зная периметр помещения, нам нужно схематически изобразить его на бумаге. Нужно нарисовать максимально похожий на комнату эскиз и разделить его на правильные фигуры, квадратуру которых легко рассчитать: треугольники, квадраты, прямоугольники и сектора. Подписываем каждое измерение на эскизе и вычисляем площади полученных фигур:

• Чтобы найти площадь треугольника, нужно перемножить длины его катетов и разделить на 2.
• Для сегмента: нам нужно взять его радиус R и умножить на половину длины дуги L.
• Для круга нужно его радиус возвести в квадрат и умножить на число пи. Оно равно примерно 3,14 и имеет постоянную величину.

Для простоты расчета площади неправильных по форме помещений в интернете сейчас можно найти онлайн-калькуляторы. Использовать их удобно: нужно выбрать планировку комнаты и ввести свои замеры, а программа автоматически рассчитает размеры комнаты. С их помощью можно быстро узнать квадратуру ванной комнаты, кухни, нестандартных жилых помещений.