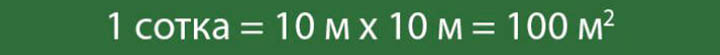Среднеквадратичное отклонение

Оценка точности результатов измерений

Оценить точность каких-либо измерений – это значит определить на основе полученных результатов сравнимые числовые (количественные) характеристики, выражающие качественную сторону самих измерений и условий их проведения. Количественные характеристики измерений или критерии оценки точности измерений устанавливаются теорией вероятности и теорией ошибок (в частности, способом наименьших квадратов). Согласно этим теориям оценка точности результатов измерений производится только по случайным ошибкам.

Показателями точности измерений могут служить:

— средняя квадратическая ошибка измерений;

— относительная ошибка измерений;

— предельная ошибка измерений.

Понятие средней квадратичной ошибки введено Гауссом, и в настоящее время она принята в качестве основной характеристики точности измерений в геодезии.

Средней квадратичной ошибкой называется среднее квадратичное значение из суммы квадратов ошибок отдельных измерений. Для ее вычисления используют либо истинные ошибки измерений, либо уклонения результатов измерений от среднего арифметического.

Обозначим истинное значение измеряемой величины через X, результат измерения через l_i.

Истинными ошибками измерений Δ_i называются разности результатов измерений и истинных значений, т. е.

В этом случае среднюю квадратичную ошибку m отдельного результата вычисляют по формуле:

где n – количество равноточных измерений.

Однако в большинстве случаев практики, если не считать редких случаев специальных исследований, истинное значение измеряемой величины и, следовательно, истинные ошибки остаются неизвестными. В этих случаях для нахождения окончательного значения измеряемой величины и оценки точности результатов измерений используют принцип среднего арифметического.

Пусть l₁, l₂, . l_nрезультаты n равноточных измерений одной и той же величины. Тогда частное

называется средним арифметическим из измеренных значений этой величины.

Разность каждого отдельного результата измерения и среднего арифметического значения называется уклонением результатов измерений от среднего арифметического и обозначается буквой v:

v_i = l_i –

Пример. Отдельный угол измерен четырьмя приемами, и получены результаты:

Тогда среднее арифметическое значение угла будет

v₁v₂v₃v₄

Уклонения результатов измерений от среднего арифметического обладают двумя важными свойствами:

— для любого ряда равноточных измерений алгебраическая сумма уклонений равна нулю = 0;

— для любого ряда равноточных измерений сумма квадратов уклонений минимальна, т. е. меньше суммы квадратов уклонений отдельных измерений от любого другого значения, принятого, вместо среднего арифметического значения, = min.

Первое свойство уклонений служит надежным контролем вычисления среднего арифметического значения из результатов измерений. Второе свойство уклонений используют для оценки точности результатов измерений.

Если ошибки отдельных измерений вычисляют относительно среднего арифметического значения из результатов измерений, среднюю квадратичную ошибку отдельного результата вычисляют по формуле

Пример. Используя данные предыдущего примера, найдем среднюю квадратичную ошибку измерения угла одним приемом:

При определении средних квадратичных ошибок измерений необходимо руководствоваться следующими правилами:

1) средняя квадратичная ошибка суммы или разности измеренных величин равна корню квадратному из суммы квадратов средних квадратичных ошибок слагаемых, т. е. для выражения А = а + b — с +. + q средняя квадратичная ошибка будет равна

при равноточных измерениях, когда m_a = m_b = m_c = . = m_q:

2) средняя квадратичная ошибка произведения измеренной величины на постоянное число равна произведению средней квадратичной ошибки этой величины на то же самое число, т. е. для выражения L = kl;

3) средняя квадратичная ошибка результатов равноточных измерений прямо пропорциональна средней квадратичной ошибке одного измерения m и обратно пропорциональна корню квадратному из числа измерений, т.е.

или с учетом формулы (12):

Примеры: 1. Угол β получен как разность двух направлений, определенных с ошибками m₁ = ± 3″ и m₂ = ± 4″.

По первому правилу находим

2. Радиус окружности измерен со средней квадратичной ошибкой m_R = ±5 см.

По второму правилу находим среднюю квадратичную ошибку длины окружности

m = 2πm_R = 2 × 3,14 × 5 = ± 31 см.

3. Средняя квадратичная ошибка измерения угла одним приемом равно m = ± 8″. Какова точность измерения угла четырьмя приемами?

По третьему правилу

4. Угол β измерен пятью приемами. При этом отклонения от среднего арифметического составили: — 2″, + 3″,- 4″, +4″ и -1″. Какова точность окончательного результата?

Источник

Среднеквадратическая погрешность

Среднеквадратические погрешности aa и стр для диафрагм и сопел известны на основании ряда многочисленных экспериментов и приводятся в нормативных документах. Но оценить максимальную погрешность однократного измерения d, p и Ар всегда возможно.
 

Определение методических ошибок дискретного измерения при линейной и.| Графическое определение среднего квадрата методической ошибки дискретного измерения при ступенчатой аппроксимации.

Среднеквадратическая погрешность си дает интегральную оценку погрешности дискретного измерения контролируемого параметра и может быть принята за критерий качества контроля как при сигнализации о превышении нормы, так и при представлении информации о тенденции изменения параметра во времени.
 

Среднеквадратическая погрешность графических построений определяется по номограмме, представленной на рис. 15.16. На горизонтальной оси графика показано число интервалов построения п, определяемое в зависимости от глубины скважины L и длины интервалов построения. Ось ординат характеризует среднеквадратическую погрешность построения планового положения забоя или другой точки скважины. Масштабы построения плана указаны на соответствующих кривых.
 

Среднеквадратическая погрешность единичного измерения рассчитывается по результатам известных эталонных значений силы тяжести и измеренных гравиметром в одних и тех же точках наблюдений. Она определяет минимальную погрешность измерений, которую можно достичь данным гравиметром.
 

Соотношение между среднеквадратическими погрешностями поверяемого и образцового средства измерений влияет на значение вероятностей ошибок поверки гораздо меньше, чем величина отношения основной погрешности и среднеквадратического отклонения.
 

Поэтому точность СДВ ФРНС невелика: среднеквадратическая погрешность местоопределения достигает нескольких километров. Несмотря на низкую точность, СДВ ФРНС находят широкое применение, так как обладают практически глобальной зоной действия, неограниченной пропускной способностью и сравнительно невысокой стоимостью бортового оборудования потребителей.
 

С метрологической точки зрения более рациональны нормированные среднеквадратические погрешности. Встречаются различные виды нормировки. Мы будем оперировать преимущественно среднеквадратическои относительной погрешностью измерения, которая определяется отношением среднеквадратического отклонения оценки к истинному значению измеряемой вероятностной характеристики.
 

АЦП используют не максимальную, а среднеквадратическую погрешность a1IB A / iT2, которая примерно в 3 5 раза меньше максимальной.
 

Это результат того, что при определении среднеквадратической погрешности из малого числа наблюдений мы находим последнюю с малой точностью.
 

Показатели надежности элементов установок оцениваются средними значениями и среднеквадратическими погрешностями. Погрешности оценок показателей надежности установок, включая ущерб, вычисляются по формулам теории точности при известных погрешностях исходных данных. Следует отметить, что относительная погрешность полученных при этом результатов, как правило, не превышает относительной погрешности исходных данных.
 

В качестве критерия параметрической оптимизации иовонетрического анализатора меркаптанов выбрана среднеквадратическая погрешность ( СКП) измерения.
 

Коэффициент множественной корреляции выражения (1.92) составляет 0 951, среднеквадратическая погрешность аппроксимации равна около 6 % при изменении давления схождения в пределах от 4 2 до 70 МПа, давления — от 0 1 МПа до рсх и температуры — от 233 до 533 К.
 

Коэффициент множественной корреляции выражения (1.92) составляет 0 951, среднеквадратическая погрешность аппроксимации равна около 6 при изменении давления схождения в пределах от 4 2 до 70 МПа, давления — от 0 1 МПа до рсх и температуры — от 233 до 533 К.
 

Определим длительность цикла квантования измеряемой величины, при котором среднеквадратическая погрешность измерения среднего значения измеряемой величины не превышала бы заданного значения.
 

Что такое точность определения координат?

Границы всех земельных наделов проводятся между угловыми (характерными) точками, а положение угловых точек определяется относительно опорных межевых пунктов, разбросанных по 2-4 пункта на один кв. километр и имеющих координаты в системе GPS.

Погрешностью измерений называют разность между истинными координатами угловой точки и координатами, измеренными кадастровым инженером. Погрешность неизбежно возникает при измерениях и складывается из следующих факторов:

1. человеческий фактор;
2. неточность измерительных приборов;
3. погодные условия;
4. особенности рельефа местности.

Одной из основных величин, применяемых для расчёта погрешности, является пункт съемочного обоснования. Это точка на местности, где кадастровый инженер устанавливает измерительное оборудование, и неровности рельефа могут привести к смещению точки установки и возрастанию общей погрешности.

Любой измерительный прибор незначительно искажает измеренную им величину из-за особенностей его конструкции, а при снятии показаний с нецифровых приборов, такие показания могут расходиться у разных работников.

СПРАВКА! Величина расхождения показаний, снятых с одного и того же геодезического прибора разными кадастровыми работниками, принимается равной половине цены деления такого прибора.

Для уменьшения погрешности измерения положения одной и той же граничной точки проводят несколько раз.

Точностью определения границ называют максимальное отклонение измеренной величины от среднего значения всех измеренных величин для одного и того же поворотного пункта. Увеличение числа проведённых измерений повышает точность итоговых расчётов.

Вам нужно провести межевание участка? Но не знаете, с чего начинать и какие нюансы есть у такой процедуры?

Прочитайте эту публикацию! В ней есть необходимые ответы.

Межевание земель: допустимая погрешность

• Земли для ИЖС – 300 метров квадратных.
• В дачном строительстве – 600 квадратов.
• Земли КФК – 600 квадратов.
• Земли личных хозяйств – ЛПХ – 400 квадратных метров.
• Земли огороднических хозяйств – 400 кв.м.
• Для возведения гаражей – не более 18 квадратов.
• Земли для организации уличной торговли – не более 5 кв.м.

Тенденция того, что одна ошибка может в будущем привести к трем другим, в рамках современного землеустроения стала нормой, одновременно спровоцировав психоз среди населения, когда землевладелец утратил уверенность в законности своего права и вообще в том, что имеющийся участок действительно принадлежит ему.

Среднеквадратичная погрешность

В заключение следует определить среднеквадратичную погрешность на выходе идеального фильтра нижних частот.
 

Заметим, что определить среднеквадратичную погрешность отдельных составляющих не всегда просто. В ряде случаев необходимо ознакомиться с технологией изготовления комплектующих изделий и методикой присвоения им погрешностей с тем, чтобы обеспечить одинаковый подход при определении погрешности отдельных составляющих. Так, при изготовлении образцовых сопротивлений, последние группируются по значениям предельных погрешностей ( 6 -) — Если известен закон распределения погрешности внутри группы сопротивлений, то нетрудно определить значение среднеквадратичной погрешности.
 

Характеристика насоса IL-11 при перекачке жидкостей с вязкостью ( в Ст.

Сопоставление коэффициентов ассоциации со среднеквадратичной погрешностью показало, что только для первых четырех признаков, перечисленных в табл. 110, связь их с определением типа месторождения, не является случайной. Эти признаки и была взяты для дальнейшего исследования.
 

Мера погрешности (2.26) называется среднеквадратичной погрешностью реализации.
 

Проследим теперь, как преобразуются среднеквадратичные погрешности при производстве математических операций. Величины, над которыми производятся операции, будем предполагать независимыми в том смысле, как это указывалось ранее.
 

Числа в круглых скобках представляют собой среднеквадратичные погрешности в последних цифрах.
 

В табл. 2 приведены значения среднеквадратичных погрешностей аппроксимации полос S, для различных вариантов нумерации пер: Вых линий ветвей Р, RI и Qb Рядом приведены значения среднеквадратичных погрешностей 5, полученных при аппроксимации каждой ветви в отдельности.
 

Из последнего примера следует, что среднеквадратичная погрешность эмпирической формулы, полученная без учета доверительных пределов, может быть значительно ниже, чем та, которая должна быть названа как погрешность формулы при достаточно высоком уровне доверия к результату.
 

Из последней леммы следует, что чем меньше среднеквадратичная погрешность, тем меньше рассеяние значений случайной величины около ее математического ожидания.
 

Коэффициент корреляции и уравнения регрессии для физико-механических показателей резиновых смесей и готовых протекторов.

Для определения достоверности найденной корреляционной зависимости вычислялись среднеквадратичная погрешность коэффициентов корреляции оог и отношение г 1аог, которое не должно быть менее 2 6, если зависимость достоверна. Таким образом, для уточнения технических условий на физико-механические показатели резиновых смесей следует задаться физико-механическими показателями готовой продукции, а по уравнениям регрессии вычислить аналогичные показатели резиновых смесей. Так, найденная корреляционная — зависимость позволяет повысить точность и надежность определения показателей качества продукции без дополнительных затрат.
 

Надежность полученных значений 0 характеризуется соответствующим значением среднеквадратичной погрешности, а также степенью представленности данного заместителя ( фактора) во всей совокупности установочных серий, выражаемой дробью, числитель которой равен числу серий, в которых этот заместитель ( фактор) представлен, а знаменатель равняется общему числу серий.
 

Эти величины и использованы для получения оценки среднеквадратичной погрешности.
 

Корень квадратный из этой величины носит название среднеквадратичной погрешности измерения.
 

Допустимые нормы расхождения

При проведении межевых работ по уточнению границ земельного надела или при определении места границ вновь образуемых наделов при выделе или разделе участков могут возникнуть расхождения значений площадей между отображённой в кадастровом паспорте и вновь рассчитанной.

ВНИМАНИЕ! Рассчитанная площадь надела земли с уточнёнными границами не может превышать площадь данного надела, указанную в кадастровых документах больше, чем на предельный минимальный размер земельного надела, установленный законом для данного вида земли. Минимальные размеры устанавливаются региональными и муниципальными нормативными актами с небольшими различиями в зависимости от субъекта федерации

Для большинства субъектов нормы расхождения площади в сторону увеличения после уточнения границ определены следующим образом (в зависимости от целевого назначения земель):

Минимальные размеры устанавливаются региональными и муниципальными нормативными актами с небольшими различиями в зависимости от субъекта федерации. Для большинства субъектов нормы расхождения площади в сторону увеличения после уточнения границ определены следующим образом (в зависимости от целевого назначения земель):

• участки для индивидуального строительства – 300 кв. м;
• участки для дачного строительства – 600 кв. м;
• участки под крестьянские хозяйства – 600 кв. м;
• участки под ЛПХ – 400 кв. м;
• наделы для огородничества (без права строительства) – 400 кв. м;
• земли под гараж – 18 кв. м;
• места под уличную торговлю – 5 кв. м.

Величина допустимых норм расхождения может быть уменьшена до 2-х раз местным законодательством, в зависимости от ситуации в регионе.

Мнение эксперта

Васильев Олег Борисович

Как видно из часто повторяющихся вопросов, чаще всего споры вызывают отклонения от установленных границ в ту или иную сторону, вопросы при межевании между соседями. Следует при этом знать, что есть допустимые погрешности, превышение которых требует приведение в надлежащий порядок:

• в случае технической ошибки (замеров, вычисления, оформления), то через проводивших замеры или Росреестр,
• в иных случаях — досудебное и судебное урегулирование.

В данной ситуации необходимо руководствоваться статьями 39 и 40 закона «О кадастровой деятельности» от 24.07.2007г. N 221-ФЗ.

7Москва

Мнение эксперта

Васильев Олег Борисович

Многолетний опыт в разных областях юриспруденции

Как видно из часто повторяющихся вопросов, чаще всего споры вызывают отклонения от установленных границ в ту или иную сторону, вопросы при межевании между соседями. Следует при этом знать, что есть допустимые погрешности, превышение которых требует приведение в надлежащий порядок:

• в случае технической ошибки (замеров, вычисления, оформления), то через проводивших замеры или Росреестр,
• в иных случаях — досудебное и судебное урегулирование.

В данной ситуации необходимо руководствоваться статьями 39 и 40 закона «О кадастровой деятельности» от 24.07.2007г. N 221-ФЗ.

Что делать в случае спорной границы

При проведении межевания возможно появление ошибок, которые могут привести к

наложению границ смежных участков и, таким образом, сократить площадь данного ЗУ.

При обнаружении такой ошибки вначале надо обратиться в ГКН. По закону эти ошибки должны исправлять сотрудники ГКН. Но если в ГНК сочтут ошибку несущественной, то собственник ЗУ может получить отказ в ее исправлении.

В этом случае на первом этапе собственник должен попытаться решить вопрос без суда.

Для этого он должен обратиться к соседу, участок которого расширился за счет ошибки, и в ГНК с просьбой исправить ошибку без судебного рассмотрения.

Такой подход может иметь положительный результат, если:

• сосед согласится с доводами потерпевшего и решит совместно провести новое межевание;
• ГНК согласится исправить ошибку в документации.

Если такой путь окажется неосуществим, необходимо подавать иск в суд. Запрос в суд должен иметь два пункта:

1. Совместно с соседом провести новое межевание и восстановить границы ЗУ.
2. Исправить ошибку в кадастровых записях.

Перед подачей иска необходимо собрать все документы, в том числе письменное подтверждение попытки примирения без суда. Важными документами будут заключение кадастрового инженера и выписка из кадастра о существующих границах ЗУ.

Зачем некоторые собственники квартир приходят пониманию необходимости расприватизации своей недвижимости? Узнайте об этом интересном моменте здесь.

Рейтинг самой дорогой недвижимости в мире представлен в нашей статье.

Погрешность при измерении площади земельного участка

• квалификация инженера-геодезиста;
• точность геодезического прибора;
• применяемый метод измерений;
• внешние условия — рельеф местности, сезон года, погодные условия в момент проведения замеров.

Основная задача инженера-геодезиста в том, чтобы при проведении замеров уложиться в разрешенные законом граничные величины погрешности. Именно эти данные прояснят ситуацию и ответят на вопрос — была ли сделана кадастровыми инженерами, которые проводили замеры ранее, принципиальная ошибка. Исчисления проводятся на основании выявления координат поворотных (характерных) точек ЗУ.

Они установлены на законодательном уровне и разнятся для земель различного назначения. Допустимая погрешность при межевании земельных участков Закон определяет, какая погрешность при межевании земельных участков считается допустимой, а какая аннулирует данные в правоустанавливающих документах на землю по причине несоответствия законодательным нормам. Особенность в том, что установление точных координат поворотных точек ЗУ невозможно в принципе.

Геодезисты знают, что при проведении межевых работ на одной и той же местности в отношении одного и того же участка будет каждый раз давать разные результаты. Это нормально. Главное, чтобы полученные цифры укладывались в норму погрешности. Какие ошибки измерения надела считаются допустимыми:

• в городах не более 10 см;
• в сёлах – 20 см;
• для земель фермеров и сельского хозяйства – 250 см;
• для стратегически важных объектов – 50 см;
• заводы и иные объекты промышленности – 150 см;
• территории заповедников и лесов – 500 см.

Именно такие стандарты установлены для межевания земельных участков, поэтому если кадастровый инженер ошибся в размерах в этих пределах, межевой план будет считаться действительным и иметь юридическую силу. Владелец надела в любой момент может изменить для земли её категорию, в этом случае иногда требуется дополнительное межевание. Обычно в таком случае в кадастровом паспорте ставится специальная отметка о том, что межевание происходило с целью уточнения границ надела. Например:

• особенности измерительных приборов;
• условия месторасположения;
• профессиональные навыки рабочего.

Именно с этой целью государством и установлены допустимые ошибки в межевых планах. Любое межевание должно быть проведено только в пределах установленных значений. Аппаратура в наше время довольно современная, поэтому обычно ошибки не превышают 5 см.

Когда нужно восстановить утраченные границы надела, сотрудник должен правильно перенести поворотные точки по указанным координатам с электронных носителей на саму местность. Чтобы избежать серьёзных ошибок в выставлении точек, некоторые компании пользуются не только данными из кадастра недвижимости, но и информацией со спутников и иными приборами. Каждая поворотная точка, обозначается на участке видимым знаком.

Обычно для этого используют специальные деревянные колья.

Сен 10, 2019adminlawsexp

Пример вычисления стандартного отклонения оценок учеников

Предположим, что интересующая нас группа (генеральная совокупность) это класс из восьми учеников, которым выставляются оценки по 10-бальной системе. Так как мы оцениваем всю группу, а не её выборку, можно использовать стандартное отклонение на основании смещённой оценки дисперсии. Для этого берём квадратный корень из среднего арифметического квадратов отклонений величин от их среднего значения.

Пусть оценки учеников класса следующие:

2, 4, 4, 4, 5, 5, 7, 9.{\displaystyle 2,\ 4,\ 4,\ 4,\ 5,\ 5,\ 7,\ 9.}

Тогда средняя оценка равна:

μ=2+4+4+4+5+5+7+98=5{\displaystyle \mu ={\frac {2+4+4+4+5+5+7+9}{8}}=5}

Вычислим квадраты отклонений оценок учеников от их средней оценки:

(2−5)2=(−3)2=9(5−5)2=2=(4−5)2=(−1)2=1(5−5)2=2=(4−5)2=(−1)2=1(7−5)2=22=4(4−5)2=(−1)2=1(9−5)2=42=16{\displaystyle {\begin{array}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(7-5)^{2}=2^{2}=4\\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16\\\end{array}}}

Среднее арифметическое этих значений называется дисперсией:

σ2=9+1+1+1+++4+168=4{\displaystyle \sigma ^{2}={\frac {9+1+1+1+0+0+4+16}{8}}=4}

Стандартное отклонение равно квадратному корню дисперсии:

σ=4=2{\displaystyle \sigma ={\sqrt {4}}=2}

Эта формула справедлива только если эти восемь значений и являются генеральной совокупностью. Если бы эти данные были случайной выборкой из какой-то большой совокупности (например, оценки восьми случайно выбранных учеников большого города), то в знаменателе формулы для вычисления дисперсии вместо n = 8 нужно было бы поставить n − 1 = 7:

σ2=9+1+1+1+++4+167≈4,57{\displaystyle \sigma ^{2}={\frac {9+1+1+1+0+0+4+16}{7}}\approx 4,57}

и стандартное отклонение равнялось бы:

σ=4,57≈2,14{\displaystyle \sigma ={\sqrt {4,57}}\approx 2,14}

Этот результат называется стандартным отклонением на основании несмещённой оценки дисперсии. Деление на n − 1 вместо n даёт неискажённую оценку дисперсии для больших генеральных совокупностей.